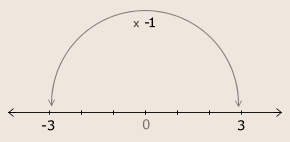
The Negative Number Line
Of course, we don't typically use the symbol i for the value 0 - 1. We write instead -1, just as we abbreviate:
2i, 3i, 4i ...
as:
-2, -3, -4 ...
And we have grown so familiar with these that we don't think of them as imaginary at all, but simply as the negative numbers.
The genius of the negative numbers is not just in their conception, but in harmonizing the rules of arithmetic to accommodate them. The negative numbers only joined the integers fully when it was realized that they formed a mirror world of numeration that took the old number line:
0, 1, 2, 3 ...
and extended it symmetrically in the opposite direction:
... -3, -2, -1, 0, 1, 2, 3 ...
This not only clearly represents the relation between the two kinds of numbers, it allows them to be arithmetically combined in a satisfying way. Addition is "movement" to the right (the direction of increase), and subtraction is movement leftward (the direction of decrease).