e

Complex Numbers Compactly

We're not through mining e^x yet. A little calculation with 2i, 3i and so forth in the formula for e^x will show that:

e²ⁱ = cos (2) + i sin (2)
e³ⁱ = cos (3) + i sin (3)

And in general:

e^xi = cos (x) + i sin (x)

This shows, at last, that e^x indeed combines the virtues of the sine and cosine functions into one: the perfect tool for compact representation of complex numbers. A complex number a + bi is some point that marks off an arc length of θ on a circle, and can be written:

cos (θ) + i sin (θ)

which is the same as:

e^iθ

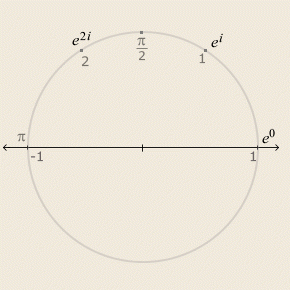
Put another way, the imaginary powers of e trace the unit circle (see the diagram at right).

Euler's Formula

Most importantly for us, the formula for e^ix leads directly to Euler's formula. π is the half-circle arc:

So at last:

e^iπ = cos (π) + i sin (π)
e^iπ = −1 + i×0
e^iπ = −1

Q. E. D.