Functions whose graphs are curves have varying slopes, and thus more complicated derivatives. The graph of y = x² looks roughly like:

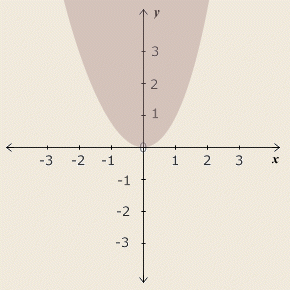
The slope starts gently and increases. At 0, it's flat. As x increases to about ½, it has begun to rise; at 1 it rises more steeply. At 2 it's steeper still — the y value runs right off the graph.

Since the slope varies as x increases, the derivative of x² will vary with x as well. Actual calculation would reveal that the function's rate of change is 2x:

Like the slope, the value of the derivative 2x increases as x does: it starts starts flat and steadily increases.

If our curve had been the cubic y = x³, its rate of increase would have been even sharper. It should have a markedly higher derivative, then, and it does:

In general the derivative of any power function is a function of the next lower power:

Note well the pattern: the multiplying factor mimics the power of the original function.