The derivative of a function is a measure of its rate of change: how the function value y changes with increasing x. When the function is graphed, the slope of the function indicates its rate of increase.

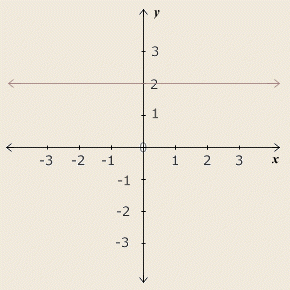
Above is the simple function y = 2. For every x, it has the value 2. Since the function's value never increases, its derivative is zero. Visually, its graph is a flat line with no slope at all.

Hence the derivative of 2 with respect to x is zero:

If this function had been y = 3, its graph would have looked much the same: a flat line at 3 instead of 2. A different line, but its slope would be the same: none at all. Its derivative, too, is zero:

By extension, the derivative of any such constant function is zero. That is, for all numbers n: