Mathematics on the curve is the domain of pi, and is accomplished not by the descendents of addition but by two new functions, sine and cosine, that serve as bridges between a point on a circle and a point on the number line.

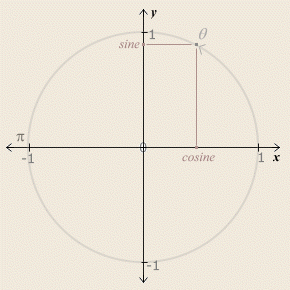
A point that lies some distance θ along the circular arc is uniquely identified by its corresponding vertical (sin θ) and horizontal (cos θ) distance along the line of each axis.

A simple relation; but note the strangeness of these two new functions. They take perfectly ordinary values such as 1 and turn them into transcendental values:

Yet for a exotic value such as π, they produce the most ordinary values imaginable:

No other math function produces such a disparity in the classes of numbers it deals in. Sine and cosine are the gateway to exactly the transcendental values missing from the real number system, and they also reveal another link between three of the constants that figure in Euler's formula:

• The square root function links i and -1, and
• The cosine function links -1 and π.

Even better, because they relate one point to a pair of numbers, the trigonometric functions are a link to the complex numbers as well.