Numbers Real and Imaginary

Here's the preferred interpretation of 3 + 2i:

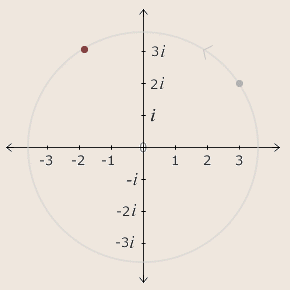
Viewing the real and imaginary parts of a complex number as coordinates of a single point takes mathematics off the lines and into the plane. This is not just a novel interpretation; it molds the mathematics of complex numbers to geometric behavior with uncanny perfection. To see how, we can multiply 3 + 2i by i:

The result, −2 + 3i, is the new point:

Note its relation to the original: multiplication by i has rotated this value in the complex plane just as the number 1 was rotated. Three more such multiplications and it would return to its original position.

This remarkably circular behavior, emerging from nothing more than the definition of i² = −1 and the arrangement of the complex plane, constitutes something of a minor mathematical miracle. It's the first strong hint of the close kinship between i and π.

«	9	»